Исследование непрерывности функции: простая задача со сложными нюансами

Каждый, кто сталкивался с математическим анализом, определенно знаком с понятием непрерывности функции. Это свойство для нее является одним из основных и, что немаловажно, позволяет судить и о других ее качествах. Именно поэтому данная задача является настолько распространенной в матанализе.

Понятие «непрерывности»

Непрерывные функции являют собой основной класс функций, которые исследуются в сфере математического анализа. При этом для простоты восприятия их можно себе представить в виде непрерывного графика, который можно начертить, не отрывая карандаш от бумаги. Таким образом, функция непрерывна для всех значений данного отрезка, в случае, если она непрерывна для всех точек x данного отрезка, то есть должно выполняться следующее равенство:

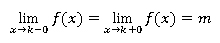
С ее помощью можно выразить одно свойство, которое очень часто встречается на практике, а именно: небольшое увеличение независимой переменной соответствует небольшому увеличению зависимой от нее переменной. Это правило используется в различных законах движения тел, к примеру, зависимость пройденного пути от времени: s = f(t).

Примерами непрерывной функции также могут послужить хорошо знакомые из школьного курса sin x, cos x, lg x и другие. Как правило, если с ними совершать какие-либо действия (умножать, вычитать, делить, складывать), то результатом снова будет непрерывная функция. Исключение составляют только те варианты, где знаменатель обращается в нуль.

Разнообразные нюансы исследования этой сферы математического анализа являются частыми вопросами для обсуждения на специализированных математических форумах. К примеру, на сайте http://www.cyberforum.ru/mathematics/ можно создавать соответствующие ветки и консультироваться с более опытными форумчанами по широкому спектру проблем матанализа.

Основной алгоритм исследования непрерывности

Определение непрерывности функции является важным для последующего построения ее графика. Однако сегодня такие задачи с успехом решаются специализированным программным обеспечением. И все же, основной алгоритм выполнения такого задания нужно знать каждому. Его можно представить в виде таких этапов:

1. поиск области определения функции;
2. установление точек разрыва и областей непрерывности;
3. исследование односторонних пределов в точках разрыва;
4. определение характера точек разрыва;
5. вычисление предела;
6. определение точек пересечения функции с осями координат;
7. построение графика.

При этом, важно понимать, что если в той или иной задаче речь идет о непрерывности функции, то она непрерывна либо в какой-то точке, либо на отрезке, интервале или полуинтервале. В любом случае, основополагающим принципом является ее непрерывность в точке.

Исследование функции на непрерывность таит в себе множество нюансов, поэтому важным является изучение всех тонкостей и технических приемов для решения подобных задач. Однако если возникают какие-либо сложности с такой математической задачей, то на портале http://www.cyberforum.ru/mathematical-analysis/ можно узнать много полезной информации из этой и любой другой сферы матанализа.